FlashAttention Algorithm

Summary

When implementing the Transfomer algorithm used in large language models to compute an output, the softmax function is used to convert the output of the matrix multiplication of the Query matrix (S X D matrix; where S is the number of tokens, and D is the dimension of the word vector) and transpose of the Key matrix (S X D).

The softmax function shown below requires that you add all the exponential of values in a given row (or column).

$$\phi(Z_i) = \frac{e^{Z_i}}{\sum_{j=1}^{K} e^{Z_j}}$$

Where i is the ith row (token #), and j is the jth column (word vector) of the word vector of size K. $ \phi(Z_i) $ is the ith score of the score matrix.

However, given the score matrix is quite large in size (S X S matrix where S usually becomes 1000~), an innovative way to compute the softmax function was developed called FlashAttention. The algorithm is shown below in figure 1:

Figure 1: FlashAttention algorithm provided in the paper.

Details of the Algorithm

The python implementation is given below:

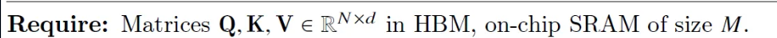
# Flash Attention

# import libraries
import torch
import torch.nn as nn

# set random seed
torch.manual_seed(42)

# set dimensions
S = 12 # number of tokens
D = 8 # word vector dimension (assume Q,K,V are square matrices)
M = 72 # Size of High Bandwidth Memory in GPU

# randomly generate the query matrices
Qmatrix = torch.rand(S,D) # query matrix
Kmatrix = torch.rand(S,D) # key matrix
Vmatrix = torch.rand(S,D) # vector matrix

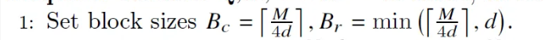
# 1. Set block sizes Bc = M/4D, Br = min (M/4D, d)
Bc = int(M / (4*D))
Br = min(int(M / (4*D)), D)

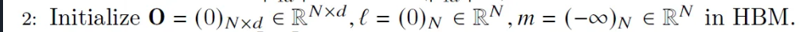
# 2. initialize output, sum of exponentials, and rowmax in HBM
m_i = torch.tensor([-float('inf')] * S)
l_i = torch.zeros(S)
O = torch.zeros(S,D)

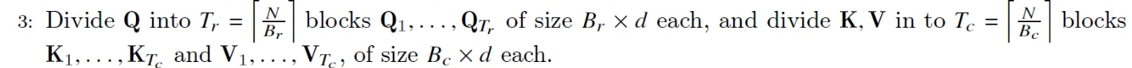
# 3. Divide Q into Tr (S/Br) blocks of size Br X d each and divide K,V into Tc (S/Bc) blocks of size Bc X d each. 

# Divide the Q into Tr blocks of size Br X D
Tr = int(S/Br)
Qblocks = Qmatrix.reshape(Tr,Br,D)

# Divide K, V into Tc blocks of size Bc X D
Tc = int(S/Bc)
Kblocks = Kmatrix.reshape(Tc,Bc,D)
Vblocks = Vmatrix.reshape(Tc,Bc,D)

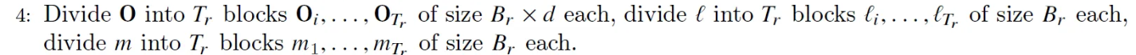
# 4. Divide O into Tr blocks of size Br X d each, divide l in to Tr blocks of size Br each, and divide m into Tr blocks of size Br each.

# Divide O into Tr blocks of size Br X D each
Oblocks = O.reshape(Tr,Br,D)

# Divide l, m into Tr blocks of size Br each
lblocks = l_i.reshape(Tr,Br)
mblocks = m_i.reshape(Tr,Br)

for j in range(Tc):
    # 6. Load Kj, Vj from the HBM to on-chip SRAM
    for i in range(Tr):
        #8. Load Qi,Oi,li,mi from HBM to on-chip SRAM
        #9. On chip, compute Sij = Qi * Kj.T
        Sij = torch.matmul(Qblocks[i],Kblocks[j].T)

        #10. On chip, compute mij = rowmax(Sij), Pij = exp(Sij - mij), lij = rowsum(Pij)

        # comptue mij = rowmax(Sij)
        mij = torch.max(Sij,dim=1).values

        # compute Pij = exp(Sij - mij)
        Pij = torch.exp(Sij - mij)

        # compute lij = rowsum(Pij)
        lij = torch.sum(Pij,dim=1)

        #10. On chip, compute minew = max(mi,mij), linew = exp(mi - minew)*li + exp(mij - minew)*lij

        # compute minew = max(mi,mij)
        mi_new = torch.max(mblocks[i],mij)

        # compute linew = exp(mi - minew)*li + exp(mij - minew)*lij
        li_new = torch.exp(mblocks[i] - mi_new) * lblocks[i] + torch.exp(mij - mi_new)*lij

        # 12. Write Oi = diag(li_new)^-1 * ( diag(li)*exp(mi -mi_new) * Oi + exp(mij - mi_new) * Pij*Vj to HBM 
        Oblocks[i] = torch.matmul(torch.inverse(torch.diag(li_new)), \
                        ( torch.matmul(torch.diag(lblocks[i]) * torch.exp(mblocks[i] - mi_new),Oblocks[i]) + \
                        torch.matmul(torch.exp(mij - mi_new) * Pij, Vblocks[j])))

        # 13. Write li = li_new, mi = mi_new
        lblocks[i] = li_new
        mblocks[i] = mi_new

O = Oblocks.reshape(-1,S,D)[0]

print("Softmax(QK.T)V:\n",O)

The above algorithm results in the same output as directly computing softmax(Q*K.T)*V in the below program:

m = torch.nn.Softmax(dim=1)
torch.matmul(m(torch.matmul(Qmatrix,Kmatrix.T)),Vmatrix)

Reference

1. Alexa Gordic. (July 2023). ELI5: FlashAttention. https://gordicaleksa.medium.com/eli5-flash-attention-5c44017022ad